题目描述
考场的炸弹危机被成功解决了,元凶被绳之以法,IOI 顺利进行。Jsp 和 Rlc 利用最后的半小时 AK 了所有题并取得了前两名。
今天是一个活动的日子,一向沉默的 Jsp 突然向 Rlc 提出了一个游戏。
「怎么了,Jsp?」
「……」
「……」
「上次的问题,你的答案又是什么呢?」
Jsp 和 Rlc 的人格魅力吸引了世界各国的 IOI 选手来玩(*)游(*)戏(*)。这其中有 $m$ 个妹子跟着 Rlc,编号为 $0,1,...,m-1$;有 $n$ 个男生跟着 Jsp,编号为 $0,1,...,n-1$。由于某些原因,总有 $m\leq n$,且 $n$ 是奇数。
现在 Rlc 准备让每个妹子选一个男生(当然,不包括 Jsp)作为同伴,一起学习 Chinese Data Structure。两个妹子不能选择同一个男生。
当然,由于语言障碍等原因妹子不是和所有男生都能愉快交流的。第 $i$ 个妹子能选择的男生可以由两个数 $a_i$ 和 $b_i$ 来描述:
对于 $0$ 到 $m-1$ 中的每个 $i$ 和 $0$ 到 $n-1$ 中的每个 $j$,若 $j$ 满足 $\min((j-a_i)\bmod n,(a_i-j)\bmod n)=b_i$(注意这里取模的值域是 $[0,n)$,如 $-1 \bmod 3 = 2$),则第 $i$ 个妹子和第 $j$ 个男生可以交流,称这对关系为 $(i,j)$。
Rlc 发现自己这边的妹子可以做到人人有同伴。但仅仅做到这一点是不行的,妹子和男生学习过程中的愉悦程度因人而异,Rlc 希望愉悦程度的总和最大。
不过某两人之间的愉悦程度有时会发生变化,这种变化一共有 $q$ 次。Rlc 用两个整数 $x,v$ 来描述变化,表示第 $x$ 对关系的愉悦程度变为 $v$。
Jsp 需要在一开始以及每次操作后回答:在所有妹子都有自己同伴的前提下,每一对同伴的愉悦程度的总和最大是多少。
有时为了强制 Jsp 按顺序回答,Rlc 会用上一次的答案加密自己对愉悦程度变化的描述。
一句话题意:在线动态维护一个二分图的最大权最大匹配。保证左侧满匹配。
输入格式
第一行三个整数 $m,n,T$。其中 $T$ 表示加密参数。
接下来一行 $m$ 个整数 $a_0,a1,...,a{m-1}$。
接下来一行 $m$ 个整数 $b_0,b1,...,b{m-1}$。
接下来一行若干个整数 $v$,按编号从小到大依次表示每对关系的初始愉悦程度。
接下来一行一个整数 $q$。
接下来 $q$ 行每行两个整数 $x',v'$,表示加密后的描述。
解密方法是:设上次答案为 $\text{lastans}$,则真实的 $x=x'-\text{lastans}\cdot T,v=v'-\text{lastans}\cdot T$。保证这个关系存在。
每对关系 $(i,j)$ 按照先 $i$ 后 $j$ 的顺序编号。即:
//no[i][j] 表示关系 (i,j) 的编号。
cnt = 0
for i = 0 to m - 1 do
for j = 0 to n - 1 do
if min((j - a[i]) mod n,(a[i] - j) mod n) = b[i] then
no[i][j] := ++ cnt
end if
end for
end for输出格式
输出共 $q+1$ 行,分别表示一开始以及每次修改后的答案。
样例 1
input
8 9 0
5 6 2 0 1 5 7 3
4 4 1 4 4 1 0 4
3 2 4 1 0 0 2 0 3 2 5 4 2 3 1
9
3 0
2 4
3 6
6 6
5 12
11 8
13 4
14 9
15 0output
19
16
17
21
27
28
29
31
31
30
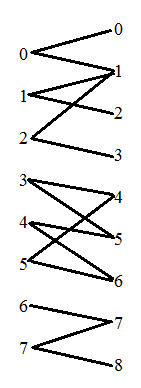
样例中描述的二分图如下:
样例 2
input
6 9 1
5 1 2 0 1 3
4 0 0 4 4 4
13 19 17 6 4 16 0 4 13 8
9
75 70
60 70
55 59
59 65
69 74
79 70
70 77
69 72
73 77output
69
57
53
53
61
70
65
65
66
66
数据范围与提示
对于所有数据,$1\leq m\leq n\leq 5\times 10^5,n$ 是奇数 $,0\leq a_i< n,0\leq b_i\leq \lfloor \frac{n}{2}\rfloor,0\leq q\leq 8\times 10^5$,任何时刻每对关系的愉悦程度是 $[0,1300]$ 中的整数。
数据保证存在一个匹配使得每个妹子都能找到自己的伙伴。
| Subtask # | 分值 | $m,n$ 的限制 | $q$ 的限制 | $T$ 的限制 |
|---|---|---|---|---|
| 1 | $7$ | $1\leq n\leq 9$ | $0\leq q\leq 9$ | $T=0$ |
| 2 | $10$ | $1\leq n\leq 18$ | $0\leq q\leq 18$ | $T=0$ |
| 3 | $17$ | $1\leq n\leq 100$ | $0\leq q\leq 100$ | $T=0$ |
| 4 | $15$ | $1\leq n\leq 5000$ | $0\leq q\leq 5000$ | $T\in{0,1}$ |
| 5 | $11$ | $1\leq n\leq 2\times 10^5$ | $q=0$ | $T=0$ |
| 6 | $13$ | $1\leq n\leq 2\times 10^5$ | $0\leq q\leq 2\times 10^5$ | $T\in{0,1}$ |
| 7 | $12$ | $1\leq n\leq 5\times 10^5$ | $0\leq q\leq 5\times 10^5$ | $T=0$ |
| 8 | $15$ | $1\leq n\leq 5\times 10^5$ | $0\leq q\leq 5\times 10^5$ | $T\in{0,1}$ |
