题目描述

一个阳光明媚的午后，ZQC 在水 QQ 群，突然他发现一位神犇发了一条装弱消息，机智的 ZQC 立即截图保存。接着，不出 ZQC 所料，群里发生了著名的“无穷递降装弱效应”。“无穷递降装弱效应”是指一位神犇装弱后，只要有一个人截图，就会发生大量的人嵌套截图的现象 ……

ZQC 对屏幕上不断滚动的嵌套截图消息十分感兴趣，他想让你帮他算一个东西。在这之前，他认为有必要再强调一些关于截图消息的概念：

一条截图消息 $M$ 可以由一个二元组 $ (u,M') $ 来表示，其中 $ u $ 是这条消息的发送者，$M'$ 是另一条截图消息或 $\mathrm{NIL}$。$ M'=\mathrm{NIL} $ 表示这条消息记录是最开始的装弱消息。

例如，这条消息（最开始的装弱消息）可以表示为 $ (A,\mathrm{NIL}) $：

而这条消息可以表示为 $ (B,(A,\mathrm{NIL})) $：

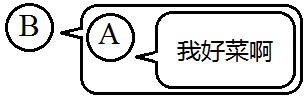
如果设第一条消息为 $ S=(A,\mathrm{NIL}) $，第二条消息也可以表示为 $ (B,S) $。

消息中一个人的出现次数定义如下： 设 $ f(M,v) $ 表示消息 $ M=(u,M') $ 中 $ v $ 的出现次数，则：

$$ f(M,v)=\begin{cases} [u=v]& M'=\mathrm{NIL}\ f(M',v)+[u=v]& M'\neq\mathrm{NIL} \end{cases} $$

其中 $[u=v]$ 这个表达式当 $u=v$ 时值为 1，否则为 0。

ZQC 终于想好要考你什么了。对于每条消息，你需要帮他算出这些：

1. 是否这条消息中所有人的出现次数都是 $3$ 的倍数。
2. 如果 1 的答案是“否”，这条消息中是否只有一个人的出现次数不是 $3$ 的倍数。
3. 如果 2 的答案是“是”，那个人是谁。

因为屏幕上的消息是一条一条发出来的，所以你也需要一条一条依序回答。

输入格式

第一行两个正整数 $ n,m $ 表示 ZQC 所在的群里有 $ n(3\leq n \leq 10^6)$ 个成员，一共发了 $ m(1\leq m\leq 2\times 10^6) $ 条消息。
接下来 $ m $ 行每行两个正整数 $u_i,M'_i$，表示第 $ i $ 条消息是 $ (u_i,M'_i) $。$M'_i=0$ 表示 $\mathrm{NIL}$，否则表示第 $M'_i$ 条消息。保证 $ 1\leq u_i\leq n,0\leq M'_i<i $。
为了体现回答的顺序性，设上次的答案为 $\mathrm{lastans}$，你需要给输入的 $u_i,M'_i$ 分别异或上 $\mathrm{lastans}$ 之后才能得到真实的输入。对于第一次询问，$\mathrm{lastans}=0$。注意，这里做异或请用 32 位有符号整数。

输出格式

输出 $ m $ 行，第 $ i $ 行一个整数表示对于第 $ i $ 条消息的计算结果。
如果 1 的答案是“是”，请输出 -1；
否则如果 2 的答案是“否”，请输出 -2；
否则，输出一个正整数表示那个人的编号。

样例 1

input

2 5
2 0
3 3
-1 -4
-1 -3
0 3

output

2
-2
-2
2
2

真实输入如下：

2 5
2 0
1 1
1 2
1 3
2 1

第 1 条消息中出现的人：${2}$，只有 $2$ 的出现次数不是 $3$ 的倍数。 第 2 条消息中出现的人：${2,1}$，$1,2$ 的出现次数都不是 $3$ 的倍数。 第 3 条消息中出现的人：${2,1,1}$，$1,2$ 的出现次数都不是 $3$ 的倍数。 第 4 条消息中出现的人：${2,1,1,1}$，只有 $2$ 的出现次数不是 $3$ 的倍数。 第 5 条消息中出现的人：${2,2}$，只有 $2$ 的出现次数不是 $3$ 的倍数。

样例 2

input

13 15
5 0
0 4
2 4
-5 -4
-8 -4
-7 -5
0 7
-6 -2
3 6
-3 -7
2 10
-5 -4
-4 -13
8 7
0 7

output

5
5
-2
-1
-2
5
-1
5
-2
3
-2
-1
3
11
11

真实输入如下：

13 15
5 0
5 1
7 1
5 2
7 3
7 5
5 2
5 1
6 3
3 7
1 9
5 2
3 12
11 4
11 12

数据范围与提示

出题人的关怀：由于输入规模较大，建议使用读入优化。