题目描述

丽贝卡是一名导游，正试图在她的杂志上介绍落基山脉。她有一张落基山脉的照片，上面排列着N(1≤N≤5000) 座山，从左向右的第 i 座山的高度是hi(1≤hi≤105)。
丽贝卡截图保留照片的一部分，这张截图的不对称性定义为：处于截图上对称位置的山的高度差的绝对值之和（截图最左和最右的山的高度差，左数第二和右数第二的山的高度差，诸如此类的和）。
丽贝卡想要知道对于长度为 i 的截图，拥有的最小不对称性。请你对于 1≤i≤N，输出这个值。

输入格式

第一行由一个整数N组成，表示图片中的山脉数量。
第二行由N个空格分隔的整数组成，其中从左起的第i个整数表示hi。

输出格式

在一行上输出N个空格分隔的整数，其中从左起的第i个整数是长度为i的截图的最对称图片的非对称值。

样例数据

input1

7
3 1 4 1 5 9 2

output1

0 2 0 5 2 10 10

样例1解释 我们以i=5为例。 第一个截图中的山脉高度为[3，1，4，1，5]，其不对称价值性为|3−5|+|1−1|+|4−4|=2。 第二个截图中的山脉高度为[1，4，1，5，9]。其不对称价值性为|1−9 |+| 4−5 |+| 1−1 |=9。 最后一个截图中的山脉高度是[4，1，5，9，2]。其不对称价值性为|4−2|+|1−9|+|5−5|=10。 因此，长度为5的最小不对称性为2。

input2

4 
1 3 5 6

output2

0 1 3 7

样例2解释 请注意，长度为4的唯一裁剪是[1，3，5，6]，其不对称值为|1−6|+|3−5|=7。

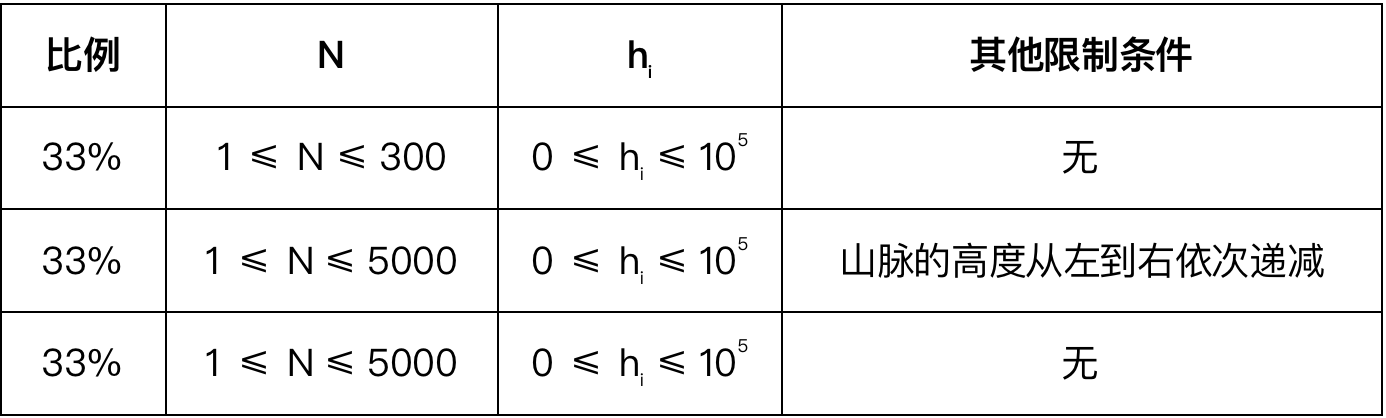
数据范围