题目描述

在一个二维平面内，给定 n 个整数点 (xi , yi)，此外你还可以自由添加 k 个整数点。 你在自由添加 k 个点后，还需要从 n + k 个点中选出若干个整数点并组成一个序列，使 得序列中任意相邻两点间的欧几里得距离恰好为 1 而且横坐标、纵坐标值均单调不减， 即 x[i+1] − x[i] = 1, y[i+1] = y[i] 或 y[i+1] − y[i] = 1, x[i+1] = x[i]。请给出满足条件的序列的最大长 度。

输入格式

第一行两个正整数 n, k 分别表示给定的整点个数、可自由添加的整点个数。 接下来 n 行，第 i 行两个正整数 xi, yi 表示给定的第 i 个点的横纵坐标。

输出格式

输出一个整数表示满足要求的序列的最大长度。

样例数据

input

8 2
3 1
3 2
3 3
3 6
1 2
2 2
5 5
5 3

output

8

其他数据详见下方附件

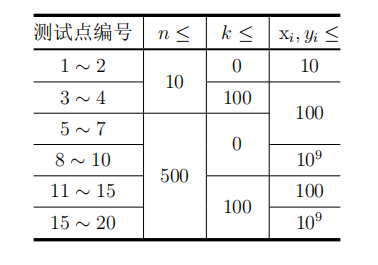
数据范围

保证对于所有数据满足：1 ≤ n ≤ 500，0 ≤ k ≤ 100。对于所有给定的整点，其横 纵坐标 1 ≤ xi, yi ≤ 10^9，且保证所有给定的点互不重合。对于自由添加的整点，其横纵 坐标不受限制。

附件下载

point.zip