题目描述
小狼新发明了一种棋盘游戏,我们暂且称它为小狼棋。游戏中有一只狼王和若干只小狼,它们会被摆在有很多方格的棋盘上。
演示一下在 8*8 的棋盘上的游戏规则。
狼王可以移动到任何一个相邻的方格,可以从下图中黑子位置到下图中白子位置,但不能超出棋盘边界。
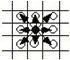
小狼可以走“日”字,(就是从下图中黑子位置移动到下图中白子位置) 也不能超出边界。
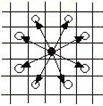
在游戏中,玩家可在每个方格上放不止一个棋子,假定方格足够大,任何棋子都不会阻碍到其他棋子正常行动。
玩家的任务就是按照上述规定,用最少步数,把所有的棋子移动到同一个方格里。另外,玩家可以选择让小狼和狼王从他们两个相遇的那个点开始一起行动,那就要遵守小狼的移动规则,其他的小狼则自己一直走到聚集地。小狼和狼王同时走的时候,只算一个走的步数。
请自行找出聚集地,并计算他们到该点的最小步数。聚集地可以在棋盘的任何位置。
输入格式:
第一行: 两个用空格隔开的整数:R,C 分别为棋盘行和列的长。不超过26列,40行。
第二行到结尾: 输入文件包含了一些有空格隔开的字母/数字对,一行有一个或以上。第一组为狼王的位置,接下来是小狼的位置。可能没有小狼,也可能整个棋盘都是小狼。行从 1 开始,列从大写字母 A 开始。
输出格式:
一行表示所有棋子到达聚集地的最小步数。
输入样例#1:
8 8
D 4
A 3 A 8
H 1 H 8
输出样例#1:
10
样例说明:
他们集中在 B5。
1号小狼: A3 - B5 (1 步)
2号小狼: A8 - C7 - B5 (2 步)
3号小狼: H1 - G3 - F5 - D4 (与狼王相遇一起走) - B5 (4 步)
4号小狼: H8 - F7 - D6 - B5 (3 步)
1 + 2 + 4 + 3 = 10 步



