题目描述

小筑是一个好学的少年，他最近无聊的在纸上画了n个塔，第i个塔的高度是hi。他会对塔进行一种操作，操作定义为在某个高度H的时候，如果第i个塔的高度高于H，我们必须把这个塔的高度变成H。这样一次操作的代价是从所有塔里面移除的1 × 1方块的总和。如果一次操作的代价小于等于k，那么就我们称这个操作为友好操作(k ≥ n)。
现在请你计算最少需要多少次友好操作，才能使得所有的塔的高度都变成相同。显然，这个肯定有答案。下面图可以参考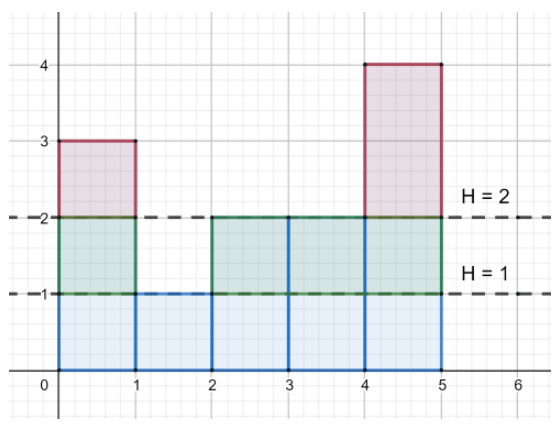 

输入格式

输入第一行是两个整数n和k，表示塔的数量和操作相关的系数k。
第二行有n个空格隔开的整数h1, h2,...hn 

输出格式

输出只有一个整数，表示最少需要的友好操作的数量，使得每个塔的高度都相同

样例数据1

input

5 5
3 1 2 2 4

output

2

样例1如图所示，需要2个友好操作，第1次设定H为2，代价为3，第2次设定H为1，代价为4

样例数据2

input

4 5
2 3 4 5

output

2

数据范围

对于50%的数据，1 ≤ n ≤2000; hi ≤ 2000。
对于100%的数据，1 ≤ n ≤ 2 ∗ 10^5; n ≤ k ≤ 10^9; hi ≤ 2 ∗ 10^5