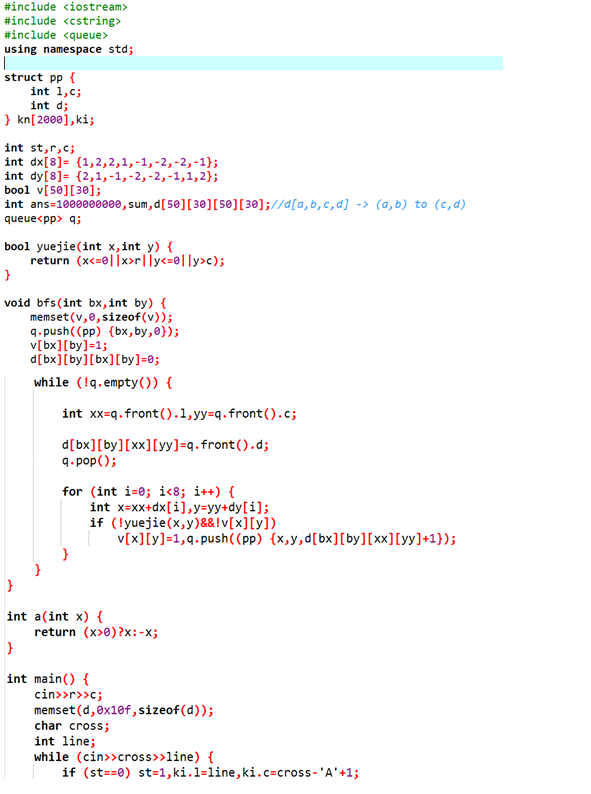
A.搭积木

首先根据数据范围来看，这道题目使用搜索肯定是行不通的。那么首先排序是一定的，假设最下面为第一层，最上面为第n层，那么从第一层到第n层每层都有a[i]种搭法，再利用乘法原理解决。但每层积木并不是可以随便摆，比如按样例中，第1层摆1，那么100就没办法摆上，所以第i层摆的积木一定要能承担还未摆放的积木中最大的一块。

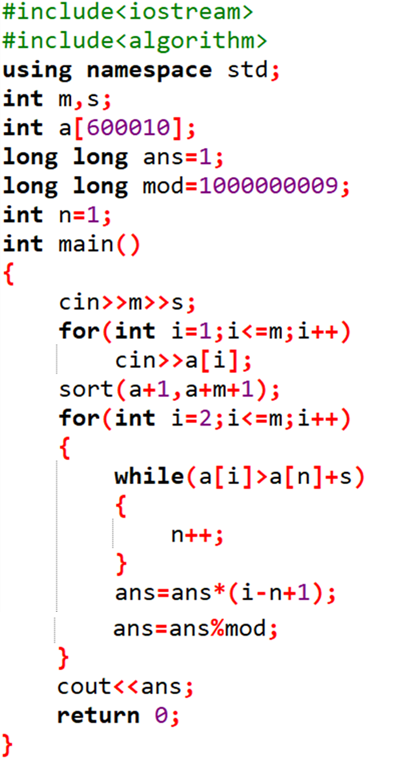
B.跳格子

这道题我们可以反向处理，反着跳格子我们就可以得出当前位置的权值是由下方、左下方或者右下方走来的。再加上问题想要获得最高分，那么我们可以选择这三个位置中的最大值再加上当前位置的权值，所以可得f[i][j]=max(max(f[i-1][j],f[i-1][j-1]),f[i-1][j+1])+a[i][j];而且题目提到，游戏开始时玩家是在最后一行的中点下面，而不是在最后一行的中点，那么在最后一行，玩家起点位置的上方、左上方、右上方都有可能被选择到，所以最后的输出结果是这三个位置的最大权值。

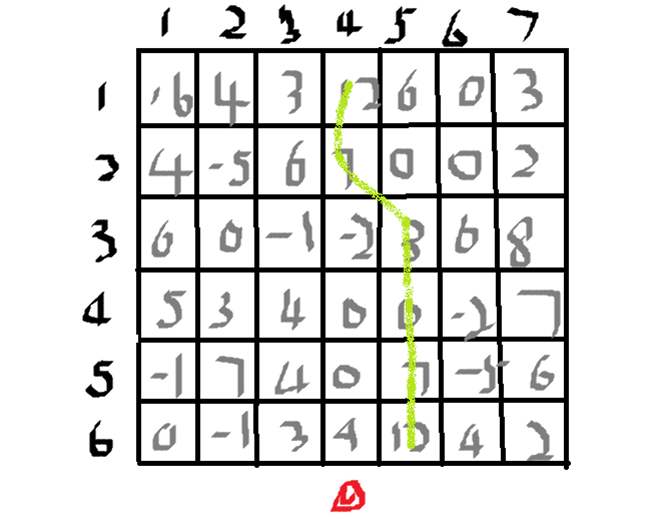
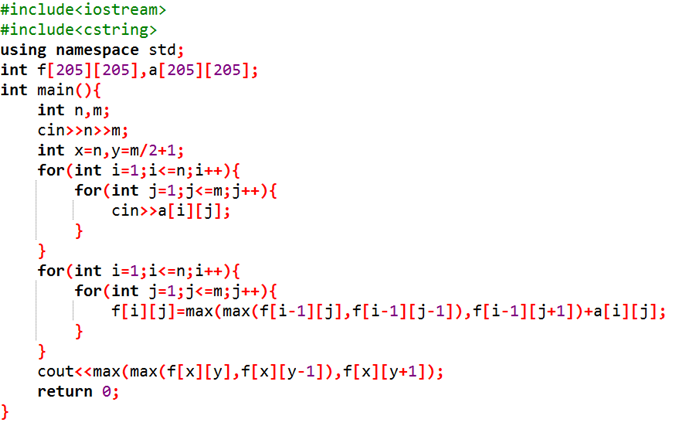
C. 破冰游戏

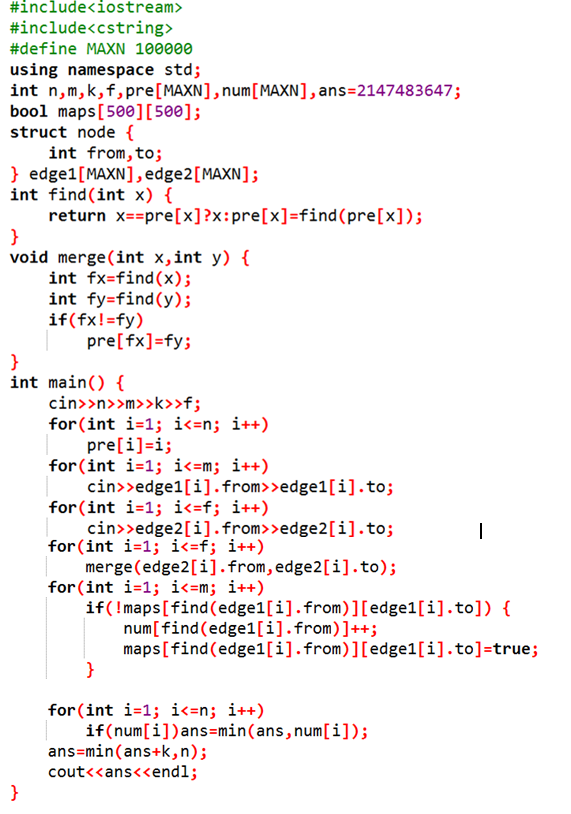
在不考虑强制玩游戏的前提下，我们可以根据样例得出这样一个关系图。女员工之间会形成几个连通块，同一个连通块中的女员工都能选择与该连通块连接的男员工一起玩游戏，比如1号女员工可以与1号男员工玩，也可以和4号男员工玩，也可以和2号男员工玩，1号女员工可以玩三轮，2号女员工可以和3号男员工玩也可以和2号男员工玩，2号女员工可以玩2轮，所以本场最多玩两轮游戏，取最小值minn。另外每个女员工还能强制k个男员工与她玩游戏，所以游戏还可以能多进行k次，即minn+k。而且显然最多只能进行n场游戏，所以找出minn+k与n之间的最小值就是答案。

D.小狼棋

先不考虑狼王，我们可以先依次枚举汇合点，用宽搜预处理出小狼在棋盘上每个能跳的点还需要多少步才能到达汇合点，但这一步处理并不是只处理最短路径，标记棋盘上所有小狼可以到达的点。 再枚举哪个小狼接（或都不接）狼王最优，得出总距离为其他小狼到汇合点的距离+“我”到国王附近的距离+国王到附近的距离+国王的附近到汇合点的距离。