有人知道系统怎么改名吗？？？

题目传送门

题目描述

一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你：蜜蜂从蜂房M开始爬到蜂房N，M<N，有多少种爬行路线？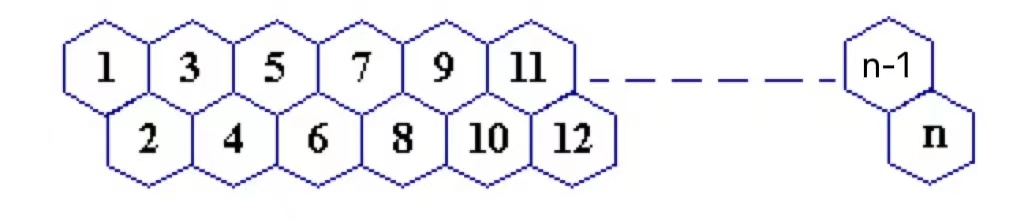

输入格式：

输入M,N的值

输出格式：

爬行有多少种路线

输入样例#1：

1 14

输出样例#1：

377

说明/提示

对于100%的数据，M,N≤1000

前言/分析

拿到题先瞪一眼：

数学$\rightarrow$标数

点开标签瞄一眼：

斐波那契$\rightarrow$高精度

$Solution1(30pts)$

根据题意，爬行的路线应为斐波那契数列的第$(n-m+1)$项

递推式为：

\begin{equation} f[0]=1,f[1]=1,f[n]=f[n-1]+f[n-2](n\geq{2},n\in{\mathbb{N^+}}) \end{equation}

数据范围为$m,n=[1,1000]$

极端情况是$m=1,n=1000$

也就是打个斐波那契数列前1000项的表就可以惹

$Code1$

#include<cstdio>
unsigned long long a[1001];
void f(){
    a[1]=1;
    a[2]=1;
    for(int i=3;i<=1000;i++)a[i]=a[i-1]+a[i-2];
}  
int m,n;
int main()
{
    f();
    scanf("%d%d",&m,&n);
    printf("%d",a[n-m+1]);
    return 0;
}

$Solution2(40pts)$

$2.1$

利用通项公式进行优化： \begin{equation} a_n=\frac{1}{\sqrt{5}}[(\frac{\sqrt{5}+1}{2})^n-(\frac{\sqrt{5}-1}{2})^n] \end{equation} 但注意精度问题，要四舍五入，且类型要强制转换成$longlong$

$Code2.1$

#include<bits/stdc++.h>
using namespace std;
int main(){
    int m,n;
    cin>>m>>n;
    cout<<(long long)(round(1/sqrt(5)*(pow((sqrt(5)+1)/2,(n-m+1))-pow((sqrt(5)-1)/2,(n-m+1)))));
    return 0;
}

$2.2$

利用矩阵进行优化：

$\left[\begin{matrix}1 & 1 \\1 & 0 \end{matrix} \right]^n$=$\left[\begin{matrix}F(n+1) & F(n) \\F(n)& F(n-1) \end{matrix} \right]$

$Code2.2$

代码出处

#include <iostream>
#include <cstddef>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
typedef vector<ll> vec;
typedef vector<vec> mat;
mat mul(mat &a,mat &b)
{
    mat c(a.size(),vec(b[0].size()));
    for(int i=0; i<2; i++)
    {
        for(int j=0; j<2; j++)
        {
            for(int k=0; k<2; k++)
            {
                c[i][j]+=a[i][k]*b[k][j];
            }
        }
    }
    return c;
}
mat pow(mat a,ll n)
{
    mat res(a.size(),vec(a.size()));
    for(int i=0; i<a.size(); i++)
        res[i][i]=1;
    while(n)
    {
        if(n&1) res=mul(res,a);
        a=mul(a,a);
        n/=2;
    }
    return res;
}
ll solve(ll n)
{
    mat a(2,vec(2));
    a[0][0]=1;
    a[0][1]=1;
    a[1][0]=1;
    a[1][1]=0;
    a=pow(a,n);
    return a[0][1];
}
int main()
{
    ll m,n;
    cin>>m>>n;
    cout<<solve(n-m+1);
    return 0;
}

www.go.helloworldroom.com:50080/problem/4534

阅读更多……

\begin{equation} \frac{-b + \sqrt{b^2 - 4ac}}{2a} \end{equation} \begin{equation} \frac{n(n+1)(2n+1)}{6} \end{equation}

\begin{equation} p= \frac{a+b+c}{2} \end{equation} \begin{equation} s= \sqrt{p({p-a})({p-b})({p-c}}) \end{equation}

嗨害嗨

嗨害嗨 我又双叒叕来了

include

using namespace std; struct student { string name; int score1,score2,total,number=1; }; int cmp(student a,student b) { return a.number>n; for(int i=0;i>a[i].name>>a[i].score1>>a[i].score2; a[i].total=a[i].score1+a[i].score2; } for(int i=0;i<n;i++) { for(int j=0;j<n;j++) { if(a[i].total<a[j].total) a[i].number++; } } sort(a,a+n,cmp); for(int i=0;i<n;i++) cout<<a[i].name<<' '<<a[i].score1<<' '<<a[i].score2<<' '<<a[i].total<<' '<<a[i].number<<endl; } 懂得都懂~

8314